(updated Oct 24 2022)
- With: Eeva Vilkkumaa (Aalto University School of Business) and Matthias Wildemeersch (IIASA)
- Academic: Published at European Journal of Operational Research (2022) – Supporting strategy selection in multiobjective decision problems under uncertainty and hidden requirements
DESCRIPTION: We developed a practical decision support framework to help with selecting strategies for complex problems. Sense making is an important outcome as well. The use of the tool is illustrated by two cases: selecting testing and lockdown strategies for controlling the COVID-19 epidemic and colorectal cancer screening programme optimization.
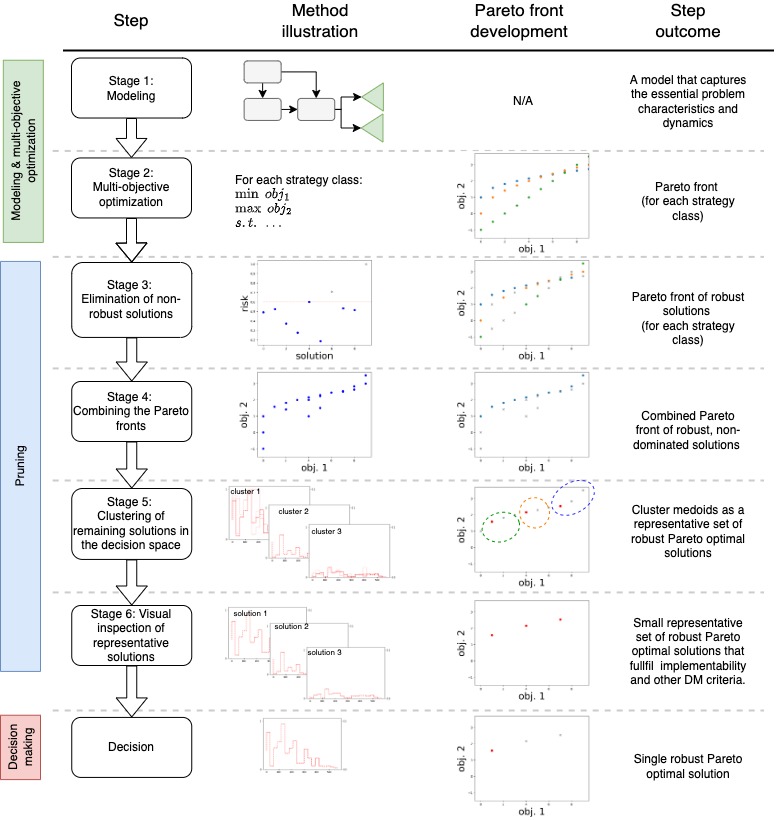
RESULTS: A step-by-step process that can be used to
- find efficient i.e. non-dominated strategies
- calculate risk estimates for them
- cluster them by their time profiles
- visualize the representative solutions of the clusters
- compare representative solutions in order to make a justified decision.
Some qualitative insights into the case problems.
APPLICATION POTENTIAL: The developed process can be used to support decision making in any situation where a process model is / can be built. It helps if a trusted system model already exists but this could be developed as a separate project.
The main steps in implementing a decision tool such as in this process would be:
- Discussion on main objectives and decision variables / alternatives
- Discussion on main risks
- Development of the process model (if not already existing)
- Integration of pymoo (or similar optimization solver) into the process model (took approx 1 week in our case)
- Setting up parallel computing (array runs) if necessary
- Experimentation and result review, iterated if necessary
MAIN TOOLS USED:
- Python + pymoo, influence diagrams + decision programming + Julia
- Triton cluster at Aalto University for running scenarios in parallel (necessity of such a cluster depends on problem)
- A compartmental COVID-19 simulator based on work by Berger & al (2020), which we extended to include imperfect tests and a contact tracing.
- A colorectal cancer screening optimization model. There will be a separate article about this.
Elaboration
This work is based on my YSSP project at IIASA. What started out as an experiment in using genetic algorithms to optimize a COVID-19 model turned into more of a methodological direction. This seems to be normal in science! The main difficulties in this project were related to problem formulation in the cases, and fine tuning and testing the framework.
The framework is meant for use in multiobjective settings, i.e. situations where several potentially conflicting objectives are maximized or minimized at the same time. The framework acts as a template for combining different algorithms into a whole, that can first find a (potentially) large set of Pareto-efficient, i.e. non-dominated solutions and then ”prune” the set so that in the end only few high quality and diverse solutions remain.
The framework is at its best:
(i) When Decision Makers (DMs) are dealing with multiple objectives, which in the absence of preference information can result in a large set of alternative solutions. In this, clustering is a useful tool that allows DMs to evaluate a reduced set of diverse and representative non-dominated solutions.
(ii) When there is considerable parametric uncertainty, which can be due to the absence of data to estimate the model parameters or to exogenous sources of uncertainty, for instance related to human behavior. The presence of model uncertainty requires us to study the robustness of non-dominated solutions.
(iii) When there are hidden requirements related to the practical implementability of the solutions that the DM finds difficult to recognize or articulate as model constraints. This requires the visual inspection of complex decision vectors for which intuition on optimality and feasibility is elusive.
(iv) When there exists time pressure to provide solutions expeditiously, preventing multiple interactions between DMs and system modelers. These time constraints can cause additional model uncertainty, stressing the need to analyze the robustness of non-dominated solutions.
There are plenty of such situations in environmental and economic modeling and in health care at least. However, the computational requirements are not trivial. The optimization and risk analysis parts may require quite a lot of computation. The framework does not add memory requirements but in many cases the same model probably has to be run for thousands or more times to produce risk estimates. And optimization takes its share of resources too. So access to e.g. a computing cluster is helpful.
For more information on this project, please email me: lauri ät laurineuvonen.fi